Potencia y amplitud: vatios, voltios y decibelios referenciados

Introducción
En aplicaciones de radiofrecuencia (pero también en muchas otras aplicaciones) es muy común tratar con señales muy grandes y muy pequeñas. Por ejemplo, un transceptor puede transmitir una potencia de 100 W y recibir solo 10 fW (o 0.000'000'000'000'01 W). Estos niveles de potencia extremadamente diferentes pueden compartir los mismos circuitos. Por supuesto, estas cifras se pueden expresar en vatios usando la notación de ingeniería (como arriba) o con la notación científica, como 1 · 102 W y 1 · 10 – 14 W, pero son bastante difíciles de pronunciar y si el exponente está mal escrito , el error resultante será enorme.

Otra forma es tomar el logaritmo y convertir todas las potencias en dBm. 100 W se convierte en + 50 dBm y 10 fW se convierten en –110 dBm: estas cifras son mucho más fáciles de manejar de memoria y de escribir. Luego, si la atenuación y la ganancia de diferentes bloques de circuito también se expresan en dB, para encontrar la potencia final, uno simplemente puede agregar todo en lugar de multiplicarlo, simplificando aún más los cálculos.

No todos se sienten cómodos con dB, dBm y unidades similares (pseudo): no hay una necesidad estricta de usarlos, pero son tan utilizados en ingeniería que es muy difícil evitarlos.

Alguna teoría
Los decibelios (dB) se usan para expresar relaciones de potencia de forma logarítmica, de modo que se pueden comparar potencias muy grandes y muy pequeñas usando números cómodos. Un decibelio es una pseudounidad adimensional porque está definida por la relación de dos poderes. Pero dado que los decibelios son tan útiles, para expresar el verdadero poder en lugar de solo una relación adimensional, los decibelios referenciados se usan con mucha frecuencia.

Si hablamos de potencia, la siguiente ecuación define el nivel de potencia P en dB de la potencia p en W referida a la potencia p0:

El factor 10 se debe a que los decibelios son "la décima parte de las campanas". Pero nunca escuché de ninguna medición realizada en Bells, solo se usan decibelios.

La unidad más común es el dBm (se pronuncia "dBm") también conocido como dBmW o decibel-milivatio: es solo el nivel de potencia en dB en comparación con una potencia de referencia de p0 = 1 mW. A veces también se usan dBW y expresan la relación de potencia relativa a p0 = 1 W, pero no son muy comunes.

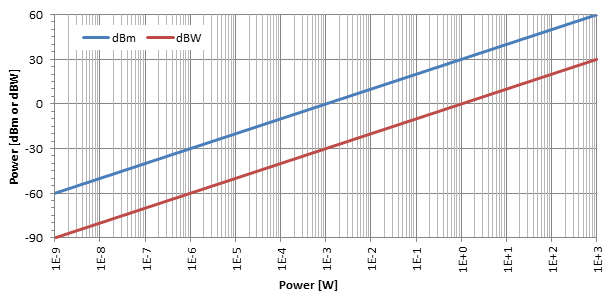
Como se muestra en la gráfica anterior, el efecto logarítmico de la conversión de decibelios es bastante evidente. Como se puede ver en este gráfico de log-lin, dBm y dBW son solo dos líneas rectas separadas por 30 dB: para convertir dBm en dBW simplemente reste 30.

En algunos dominios, como la recepción de TV analógica, es común medir el voltaje en lugar de la potencia. Esto no es un problema siempre que la impedancia sea conocida y fija (los receptores de TV usualmente usan 75 Ω).

Los voltajes absolutos también pueden aprovechar la escala logarítmica de decibelios usando decibelios-microvoltios (dBμV) y decibelios-voltios (dBV). El más común es el dBμV que expresa la relación de voltaje en relación con u0 = 1 μV. A veces también se usan dBV y expresan la relación de voltaje con respecto a u0 = 1 V.

Tenga en cuenta que los voltajes usan un "20" en lugar de un "10" en su fórmula de dB. Esto se debe a que los decibelios siempre se definen como raciones de poder; Si solo tenemos voltajes, primero debemos cuadrarlos para encontrar el poder. Esa potencia de dos, cuando se saca del logaritmo, multiplicará el factor existente de 10 por 2.

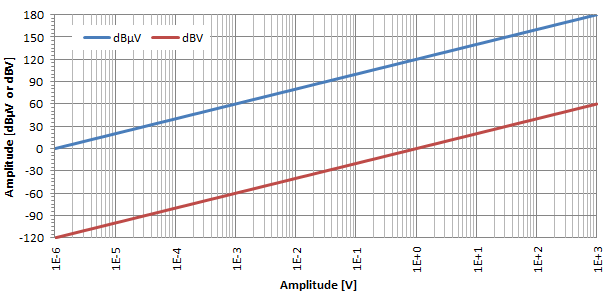
Como se muestra en la gráfica anterior y de una manera similar a la anterior, el efecto logarítmico de la conversión de decibelios es bastante evidente también para los voltajes. Como se puede ver en este gráfico de log-lin, dBμV y dBV son solo dos líneas rectas separadas por 120 dB: para convertir dBμV en dBV simplemente reste 120.

Ahora, si queremos convertir de potencia a voltaje y viceversa, necesitamos saber la impedancia. Solo usamos la siguiente ecuación:

Esta conversión solo es válida cuando la impedancia Zc es real y la carga coincide con la línea de transmisión.

Si graficamos el nivel de potencia en dBm y el nivel de amplitud en dBμV en función de la potencia en W para una impedancia dada (aquí Zc = 50 Ω) obtenemos lo siguiente:

Como antes, tenemos dos líneas paralelas 107 dB separadas. Entonces, para convertir de dBm a dBμV, simplemente agregue 107 dB para Zc = 50 Ω, agregue 109 dB para Zc = 75 Ω, agregue 115 dB para Zc = 300 Ω o agregue 118 dB para Zc = 600 Ω.

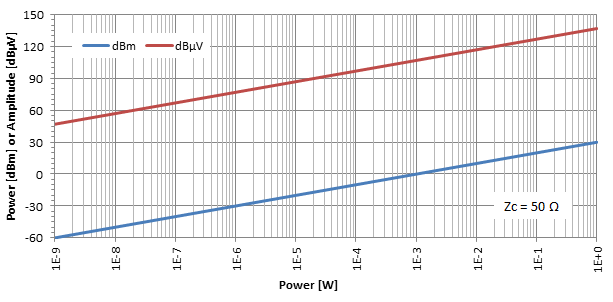
Consideraciones prácticas
A primera vista, uno puede pensar que debido al logaritmo, una calculadora de bolsillo es absolutamente necesaria para manejar dBm. En realidad, un cálculo aproximado se puede hacer fácilmente en su cabeza. Tienes que recordar solo tres hechos:
 Una potencia de 1 mW es 0 dBm.
 Cada vez que se duplique la potencia, agregue 3 dB.
 Cada vez que la potencia aumenta en un factor de 10, agregue 10 dB.

Ahora, consideremos algunos ejemplos: supongamos que tenemos un nivel de potencia de 26 dBm. Podemos escribir 26 dBm = 0 dBm + 10 dB + 10 dB + 3 dB + 3 dB, y con las tres reglas simples anteriores, podemos encontrar fácilmente la potencia haciendo 1 mW · 10 · 10 · 2 · 2 = 400 mW .

Otro ejemplo: supongamos que tenemos –33dBm: podemos escribir como –33 dBm = 0 dBm - 10 dB - 10 dB - 10dB - 3 dB, y encontramos 1 mW / 10 / 10 / 10 / 2 = 0.5 μW.

Esto también funciona al revés, por ejemplo, 50 mW son solo 1 mW · 10 · 10 / 2. En dBm tenemos 0 dBm + 10 dB + 10 dB –3 dB = 17 dBm.

Esto requiere algo de práctica, pero es muy fácil de hacer. No es tan preciso como una calculadora de bolsillo porque solo puede ser preciso a ± 2 dB pero, por el esfuerzo, da una muy buena idea de la intensidad de una señal.

Un método similar también funciona para dBμV, pero las reglas son diferentes:
 Una amplitud de 1 μV es 0 dBμV.
 Cada vez que la amplitud se duplique, agregue 6 dB.
 Cada vez que la amplitud aumenta en un factor de 10, agregue 20 dB.

Puede que se sorprenda de los cálculos en decibelios mostrados anteriormente, donde se agregan dB a dBm, lo cual es bastante extraño. Esto se debe a que los decibelios son pseudounidades y no se comportan como de costumbre. La relación de dos potencias se expresa en dB pero no tiene dimensiones: por ejemplo, 3 dB solo significa "el doble". La potencia expresada en dBm es realmente una potencia: por ejemplo, 10 dBm significa "10 veces más fuerte que 1 mW", que es 10 mW.

Ahora, cuando agrega decibelios (dB, dBm, ...), debido a su naturaleza logarítmica, en realidad está multiplicando las cifras originales. Entonces, si agrega una ganancia de 3 dB a una potencia de 10 dBm, obtendrá 13 dBm. Pero lo que realmente hizo fue multiplicar un factor de 2 con una potencia de 10 mW obteniendo 20 mW, que es 13 dBm.

Hasta ahora todo bien, agregar es mucho más fácil de hacer en tu cabeza que multiplicar, y esto hace que los decibelios sean tan útiles. Pero hay un problema: dado que agregar decibelios juntos corresponde a multiplicar los factores originales, ¿cómo se puede agregar (combinar) la potencia de dos señales? Pues no puedes. No puede agregar dBm a dBm. Si, por ejemplo, tiene un circuito o un dispositivo que combina la potencia de una señal de 10 dBm (10 mW) con la potencia de otra señal de 13 dBm (20 mW), el resultado es 10 mW + 20 mW = 30 mW que es 14.8 dBm. No hay forma de hacerlo directamente en dBm, debe convertir ambas potencias en vatios, agregarlas y volver a convertirlas en dBm. Esta es una gran limitación de decibelios y una trampa común; Afortunadamente, esta operación no es muy común.

Si desea construir una estación de radio, amplíe su transmisor de radio FM o necesita cualquier otro Equipo de FM, Siéntete libre de contactarnos: [email protected].

Deja un mensaje 

Lista de mensajes