Tutorial de decibelios: dB y dBm frente a ganancia y milivatios

El concepto de un decibelio (dB) es comprensiblemente difícil y confuso para alguien que acaba de ser presentado. La combinación de especificaciones de ganancia, potencia y voltaje (y corriente, pero no con tanta frecuencia) que mezclan dB, dBm, dBW, vatios, milivatios, voltaje, milivoltios, etc., a menudo requiere la conversión de valores lineales a decibelios. Este breve tutorial ayudará a aclarar la diferencia entre trabajar con decibelios y trabajar con valores lineales.

Los logaritmos (registros) fueron concebidos por primera vez en los primeros 1600 por el matemático escocés John Napier, como una herramienta para simplificar las operaciones de multiplicación y división al convertirlos en operaciones de suma y resta más rápidas y menos propensas a errores, respectivamente. Esto es posible debido a la forma en que la multiplicación de dos números expresados ​​como números base similares con exponentes se puede lograr simplemente sumando los exponentes. La división de esos mismos números se logra restando los exponentes. Es una de las leyes de los exponentes, y se ve así:

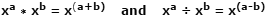
Usando números reales como ejemplo, donde x = 10, a = 4, b = 1:

La ley de exponentes funciona para cualquier número base, no solo 10. Esto es:

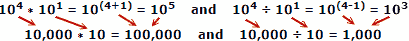
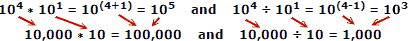
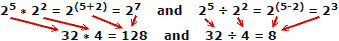
Las personas tienden a cometer menos errores al sumar y restar números, por lo que la ventaja de los logaritmos es evidente. Recuerde que los logaritmos se desarrollaron antes de que las computadoras automáticas mecánicas o electrónicas estuvieran disponibles. Una regla de cálculo explota las propiedades de los logaritmos para el cálculo, pero ese es un tema principal separado.

Esos son ejemplos simples, pero son válidos para cualquier base o exponente. En ausencia de una calculadora, para ser útil para la aplicación general, necesita una tabla de números y sus logaritmos equivalentes. Las primeras tablas de registro llenaron volúmenes, dependiendo del espaciado entre números (1.000, 1.001, 1.002, 1.003, vs. 1.0, 1.1, 1.2, 1.3, etc.). La buena noticia para los creadores de tablas de logaritmo es que solo se requiere una 'década' de números (por ejemplo, 1 a 10) ya que cada década anterior o separada es un múltiplo simple de una potencia de 10.

Nota: Utilizo la base 10 en esta discusión ya que esa es la base de nuestro sistema numérico común, de ahí el término 'logaritmo común' para los registros base 10. Es posible que haya oído hablar de logaritmos naturales, que usan la base de e, pero e no se usa con mucha frecuencia al calcular la potencia eléctrica escalar, el voltaje y las cantidades de corriente (aunque se usa cuando se incluyen ángulos de fase, es decir, la identidad de Euler). Los logaritmos naturales se escriben como ln (x) sin el subíndice 'e', ​​mientras que los logaritmos 10 básicos se escriben simplemente como log (x) sin el subíndice 10; es decir, no loge (x) o log10 (x), respectivamente.

Por una base = tabla de registro 10:

Papel cuadriculado de ingeniería semi-logarítmica 5 Cycles - RF Cafe La excepción y el caso especial es logx (0) = Indefinido. Eso es así porque no hay poder al que pueda elevar cualquier número y obtener 0 (cero). Puede acercarse asintóticamente a cero, pero no puede llegar a cero. Nunca se mostrará el número cero en una escala logarítmica; Por lo general, corren de una potencia de 10 a otra potencia de diez. Un ejemplo de papel cuadriculado se muestra a la derecha. Tiene 'ciclos' o 'décadas' de rango 5. Tenga en cuenta que no hay cero en el eje y.

El logaritmo base-10 (común) de un número, entonces, es el exponente al que se debe elevar 10 para obtener ese número. En otras palabras, dado que 10 elevado a la potencia de 2 es igual a 100 (102 = 100), el registro base-10 de 100 es 2 (log10 100 = 2).

Esta es la ley básica de los logaritmos:


Realizando las mismas multiplicaciones y divisiones que en la parte superior de la página usando logaritmos reales:



Eso está bien, pero con lo que terminas es el logaritmo del número que buscas. Pregunta: Excepto por un ejemplo simple como este, ¿cómo obtiene la respuesta que necesita? Respuesta: Busque el antilogaritmo (antilog) del resultado. En este caso:

Un ejemplo más difícil y más probable con números que no son potencias enteras de 10, podría parecerse a lo siguiente:




 Calculadora HP-35 (wikipedia) - RF Cafe Dado que el logaritmo de 'x' es igual a 1.8444, el antilog es igual a 'x', que es 69.9



Utilicé mi calculadora para buscar los registros y antilogs para esos números, pero antes de 1972 cuando Hewlett Packard (HP) presentó su calculadora científica HP-35, la persona promedio sin acceso a una computadora central corporativa o universitaria necesitaba usar un registro tabla para realizar tales cálculos.

¿Quién se molesta en usar logaritmos hoy en día? Mucha gente, incluyéndome a mí, con bastante frecuencia al calcular parámetros del sistema en cascada como la figura de ruido (NF) y los puntos de intercepción (IP). La suma y resta simples de los valores de dB de ganancia y dBm de potencia no funcionan con NF e IP. Las fórmulas de gobierno utilizan la multiplicación y división de los valores de ganancia y potencia lineales, lo que requiere convertir primero dB y / o dBm a números lineales (relación de ganancia y mW) usando antílogos, realizar los cálculos en cascada y luego convertir el resultado nuevamente a dB y / o dBm usando registros.

No todas las operaciones en cascada del sistema requieren conversión de ida y vuelta. Por ejemplo, si solo se necesita la ganancia total del sistema y / o el nivel de potencia de salida, los cálculos se pueden realizar con unidades lineales (mW y multiplicadores) o unidades logarítmicas (dBm y dB, respectivamente).

La definición de 'dB' y 'dBm'

Un decibel (dB) en ingeniería eléctrica se define como 10 multiplicado por el logaritmo base-10 de una relación entre dos niveles de potencia; por ejemplo, Pout / Pin (ganancia, en otras palabras). Esto es:

Por tanto, todas las ganancias superiores a 1 se expresan como decibeles positivos (> 0) y las ganancias inferiores a 1 se expresan como decibeles negativos (<0). Tenga en cuenta que para los casos que la mayoría de nosotros encontramos, la relación lineal de P1 / P2 debe ser un número positivo (> 0) ya que el logaritmo de 0 no está definido y el logaritmo de los números negativos es complejo (contienen tanto una parte real como una imaginaria ). El valor de dB, sin embargo, teóricamente puede tomar cualquier valor entre −∞ y + ∞, incluido 0, que es una ganancia de 1 [10 * log (1) = 0 dB].

'dBm' es una unidad de potencia basada en decibelios a la que se hace referencia en 1 mW. Dado que 0 dB de ganancia es igual a una ganancia de 1, 1 mW de potencia es 0 dB mayor que 1 mW o 0 dBm. Del mismo modo, una unidad de potencia de dBW es decibelios en relación con 1 W de potencia.


En consecuencia, todos los valores de dBm mayores que 0 son mayores que 1 mW, y todos los valores de dBm menores que 0 son menores que 1 mW (ver Fig. 1). Por ejemplo, + 3.01 dBm es 3.01 dB mayor que 1 mW; es decir, o 0 dBm + 3.01 dB = + 3.01 dBm (2 mW). −3.01 dBm es 3.01 dB menor que 1 mW; es decir, o 0 dBm + (−3.01) dB = −3.01 dBm (0.5 mW).

La siguiente tabla ofrece algunos ejemplos numéricos para que pueda ver la correlación entre mW y dBm. El mismo conjunto de valores trazados en una escala logarítmica produciría una línea recta. Debido a la relación logarítmica, el gráfico agrupa los valores más pequeños contra el eje vertical izquierdo. Se inserta una versión ampliada de la región 0 a 1 mW para mayor claridad.

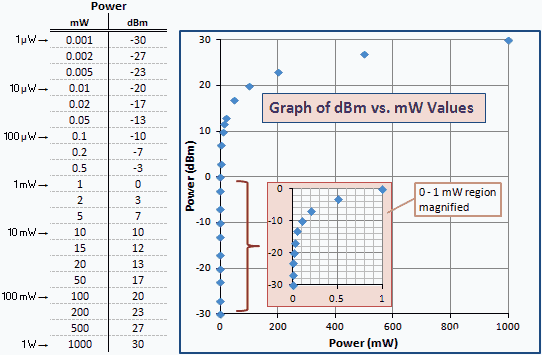
Fig. 1 - Gráfico de potencia en unidades de dBm vs. mW

La Fig. 2 es una tabla y un gráfico de dB vs. relaciones de ganancia lineal similares a los dBm vs. mW en la Fig. 1. Tenga en cuenta que los números y las curvas son exactamente iguales; solo se cambian las etiquetas del eje. Esto se debe a que dBm es una unidad de potencia expresada en dB en relación con 1 mW (0 dBm).

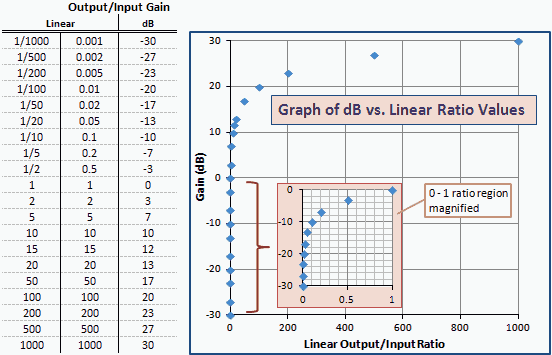
Fig. 2 - Gráfico de ganancia en unidades de dBm vs. relación lineal

Básicamente, la ganancia es un factor de multiplicación (o división). Como ejemplo, un amplificador podría tener una ganancia que aumenta la señal en un factor de 4 (es decir, 4x) de entrada a salida (ver Fig. 3). Si una señal 1 mW (0 dBm) se alimenta al amplificador, entonces 1 mW * 4 = 4 mW sale. En términos de decibelios, un factor de 4 es equivalente a 10 * log (4) = 6.02 dB, por lo que 0 dBm en más 6.02 dB de ganancia produce + 6.02 dBm en la salida.

1 mW * 4 = 4 mW

0 dBm + 6.02 dB = 6.02 dBm

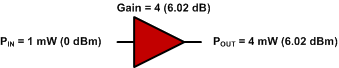
Fig. 3 - Ganancia de amplificador único.

Ganancias combinadas (lineal y dB) con valor positivo

Si un amplificador con una ganancia de 4 está en serie con un segundo amplificador con una ganancia de 6, entonces la ganancia total es 4 * 6 = 24. En términos de decibelios, un factor de 6 es equivalente a 10 * log (6) = 7.78 dB, y un factor de 24 es equivalente a 10 * log (24) = 13.8 dB.

Así como 4 x 6 = 24 (ganancia lineal), 6.02 dB + 7.78 dB = 13.8 dB (ganancia de decibelios).

Si una señal 1 mW (0 dBm) se alimenta al amplificador, entonces 4 mW sale del primer amplificador y 24 mW sale del segundo amplificador. Ver Fig. 4.

1 mW * 4 * 6 = 24 mW
0 dBm + 6.02 dB + 7.78 dB = 13.8 dBm

Fig. 4 - Ganancia de amplificador dual en cascada.

Combinación de ganancia y pérdida (lineal y dB)
El siguiente ejemplo muestra lo que sucede cuando se encuentra una ganancia <1 (una pérdida), donde se coloca un atenuador con una ganancia de 1/6 después del primer amplificador en lugar de tener un segundo amplificador. Vea la figura 5.
4 * 1 / 6 = 2 / 3 (ganancia lineal). De manera similar, 6.02 dB - 7.78 dB = −1.76 dB (ganancia de decibelios).
Como en el ejemplo anterior, si una señal 1 mW (0 dBm) se alimenta al amplificador con una ganancia de 4, entonces sale 4 mW. Ese 4 mW luego entra en el atenuador con una ganancia lineal de 1 / 6 y sale a un nivel de potencia de 4 / 6 mW (2 / 3 mW).
La ganancia total en este caso es 4 / 6 = 2 / 3, por lo que la potencia de salida será realmente menor que la potencia de entrada.

1 mW * 4 * 1 / 6 = 2 / 3 mW = 0.67 mW

0 dBm + 6.02 dB + (-7.78 dB) = −1.76 dBm

Fig. 5: ganancia del amplificador en cascada y atenuador.

12 mW + 34 mW + 8 mW + 20 dB

Información suplementaria sobre logaritmos
Logaritmos de productos
Una propiedad de logaritmos utilizada implícitamente arriba establece lo siguiente, y es la base para poder sumar y restar valores de logaritmo en lugar de multiplicar sus equivalentes lineales.

'h * j / k * m / n' podría representar una cascada de componentes que tienen tres dispositivos (h, j y m) cada uno con ganancia> 1 y dos dispositivos (kyn) cada uno con una ganancia <1 (ver Figura 6). La ganancia total del sistema se puede calcular multiplicando todos los valores de ganancia lineal juntos o sumando todos los valores de ganancia de decibelios.

Fig. 6 - Componentes en cascada

Logaritmos de exponentes
Lo siguiente es importante para comprender por qué la ganancia de potencia en términos de potencia es 10 * log (Pout / Pin) dB, mientras que la ganancia de potencia en términos de voltaje es 20 * log (Vout / Vin) dB.


lo cual es así porque cf es igual a c multiplicado por sí mismo 'f' veces. Por ejemplo, si f = 4:


Ganancia de potencia basada en potencia versus ganancia de potencia basada en voltaje
La ganancia de potencia es Pout / Pin, y la ganancia de voltaje es Vout / Vin. La ganancia de potencia basada en una relación de potencia en decibelios se define como 10 * log (Pout / Pin). La ganancia de potencia en términos de voltaje es [(Vout2 / R) / (Vin2 / R)], ya que según la ley de Ohm P = V2 / R. La 'R' en los denominadores cancela dejando Vout2 / Vin2, que es igual a (Vout / Vin) 2, según lo definido por la regla de exponentes que dice ac / bc = (a / b) c. Por lo tanto:

Nota Importante: La ganancia de voltaje en términos de voltaje es 10 * log (Vout / Vin) dB, lo mismo que con la ganancia de potencia en términos de potencia. Es solo cuando la ganancia de potencia se expresa en términos de voltaje que se aplica la ecuación 20 * log (Vout / Vin) dB. Este es un punto común de confusión.


Ninguna operación en matemáticas es arbitraria, y eso explica por qué una pérdida de potencia de la señal (ganancia <1) se representa como un valor negativo y, por lo tanto, se resta durante un cálculo en cascada. Es una demostración sencilla, pero digna de mención.

log (1 / f) = log (1) - log (f) = 0 - log (f) = -log (f)

Si desea construir una estación de radio, amplíe su transmisor de radio FM o necesita cualquier otro Equipo de FM, Siéntete libre de contactarnos: [email protected].

Deja un mensaje 

Lista de mensajes